앞선 1장에서 설명했듯, DFS/BFS는 각각 탐색 알고리즘이다. 이 탐색 알고리즘을 이해하기 위해 요구되는 선행지식은 재귀, 스택, 큐 정도이다. 만약 이 선행지식을 모르고 있다면 이전 포스팅을 참고하면 좋을 것 같다.
2024.06.29 - [LeetCode + 알고리즘] - [Algorithm] DFS/BFS(1) - DFS/BFS를 이해하기 위한 자료구조
[Algorithm] DFS/BFS(1) - DFS/BFS를 이해하기 위한 자료구조
이 유형은 코딩 테스트에서 거의 필수적으로 출제되는 유형이다. 저번에 코테를 봤을때도 DFS/BFS는 무조건 한 문제씩은 출제 되었으며, 이 문제는 어려운 난이도에 속해 합격 여부를 판가름 하는
jghdg1234.tistory.com
📌 DFS
DFS(Deapth First Search)는 깊이 탐색 알고리즘이라 불리우며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다. 이를 이해하려면 먼저 '그래프' 자료구조에 대해 알고 있어야 한다. '그래프'는 노드(node)와 간선(edge)로 구성되며, 이때 노드를 정점(vertex)라고도 한다. 그래프 탐색이란 하나의 노드에서 시작하여 다수의 노드를 방문 하는것을 말한다. 여기서 노드와 노드 사이가 간선으로 연결되어 있다면, 두 노드는 인접해있다 라고 말할 수 있다.

CS에서 그래프는 두가지 방식으로 표현 될 수 있다.
- 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현하는 방식

먼저, 인접 행렬 방식은 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식이다. 위와 같은 2차원 행렬 그래프를 파이썬에서는 2차원 배열로 구현 할 수 있다. 연결이 되지 않는 노드끼리는 무한의 비용이라고 표현한다. 실제 코드에서는 논리적으로 정답이 될 수 없는 큰 값중 99999999와 같이 초기화를 하는 경우가 많다.
INF = 99999999999999
#2차원 리스트를 이용해 인접 행렬 표현
graph = [
[0, 7, 5],
[7, 0, INF],
[5, INF, 0]
]
print(graph)
출력 결과 : [[0, 7, 5], [7, 0, 9999999999], [5, 999999999999, 0]]
- 인접 리스트(Adjacency List) : 인접 리스트 방식에서는 다음 그림처럼 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장한다.

인접 리스트는 연결 리스트(LinkedList)를 활용하여 구현하는데, 파이썬은 기본 자료형인 리스트 자료형이 append()와 같은 메소드를 제공하므로, 배열과 연결 리스트의 기능을 동시에 제공한다. 파이썬으로 인접 리스트를 구현 할 때에도 단순히 2차원 리스트를 이용하면 된다는 것을 기억하자.
# 행(Row)이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))
# 노드 1에 연결된 노드 정보 저장(노드, 거리)
graph[1].append((0, 7))
# 노드 2에 연결된 노드 정보 저장(노드, 거리)
graph[2].append((0, 5))
print(graph)
#출력결과 : [[(1,7), (2, 5)], [(0, 7)], [(0, 5)]]
아래는 리스트 컴프리헨션에 관한 내용이다.
`graph = [[] for _ in range(3)]`는 파이썬의 리스트 컴프리헨션을 사용하여 3개의 빈 리스트를 가지는 리스트를 생성하는 코드이다.
코드 설명
graph = [[] for _ in range(3)]
리스트 컴프리헨션
리스트 컴프리헨션은 기존 리스트나 다른 iterable 객체를 기반으로 새로운 리스트를 생성하는 간결한 방법이다. 일반적인 구조는 다음과 같다:
[new_item for item in iterable]
여기서 `graph = [[] for _ in range(3)]`는 리스트 컴프리헨션을 사용하여 다음과 같은 작업을 수행한다:
1. `range(3)`:
- `range(3)`은 0부터 2까지의 숫자를 생성하는 이터러블 객체이다. 즉, `[0, 1, 2]`와 같다.
2. `for _ in range(3)`:
- `for` 루프를 3번 반복합니다. 여기서 `_`는 변수로 사용되지만, 값이 실제로 사용되지 않음을 나타내기 위해 `_`로 이름을 지정한다. 이는 해당 변수가 반복문 내부에서 사용되지 않을 때 자주 사용된다.
3. `[]`:
- 반복할 때마다 빈 리스트 `[]`를 생성한다.
4. 결과:
- 3번의 반복을 통해 3개의 빈 리스트가 포함된 리스트를 생성한다.
즉, 이 코드는 다음과 같은 리스트를 생성한다:
graph = [[], [], []]
📎 위의 두 방식에는 어떤 차이가 있을까?
메모리 측면에서 살펴본다면, 인접 행렬 방식은 모든 관계를 저장하므로 노드 갯수가 많을수록 메모리가 불필요하게 낭비된다. 반면, 인접 리스트 방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다. 하지만 이와 같은 속성 때문에 인접 리스트 방식은 인접 행렬 방식에 비해 특정 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다. 인접 리스트 방식에서는 연결된 데이터를 하나하나 확인해야 하기 때문이다.
예를들어, 노드 1과 7이 연결되어 있는지 확인할때, 인접 행렬 방식에서는 graph[1][7]만 확인하면 된다. 반면 인접 리스트 방식에서는 노드 1에 대한 인접 리스트를 앞에서부터 순회해야 한다. 그러므로, 특정한 노드와 연결된 모든 인접 노드를 순회해야 하는 경우, 인접 리스트 방식이 인접 행렬 방식에 비해 메모리 낭비가 적다.
📎DFS는 어떤 방식으로 동작할까?
DFS는 우선 깊이 탐색 알고리즘 이라고 했다. 이 알고리즘은 특정한 경로로 탐색하다가 특정한 상황에서 최대한 깊숙이 들어가 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘이다. DFS는 스택 자료구조를 이용하며 구체적인 동작은 다음과 같다.
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있다면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 2의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
다음과 같은 그래프를 생각 해보자. 노드 1을 시작으로 DFS를 이용해 탐색을 한다면 이름에 걸맞게 단순히 가장 깊이 있는 노드를 탐색 할때까지 탐색하면 된다. 또한 일반적으로 인접한 노드 중에서 방문하지 않은 노드가 여러개 있으면 번호가 낮은 순서부터 처리한다.

다음은 DFS가 실행되는 로직을 도식화 한 것이다.
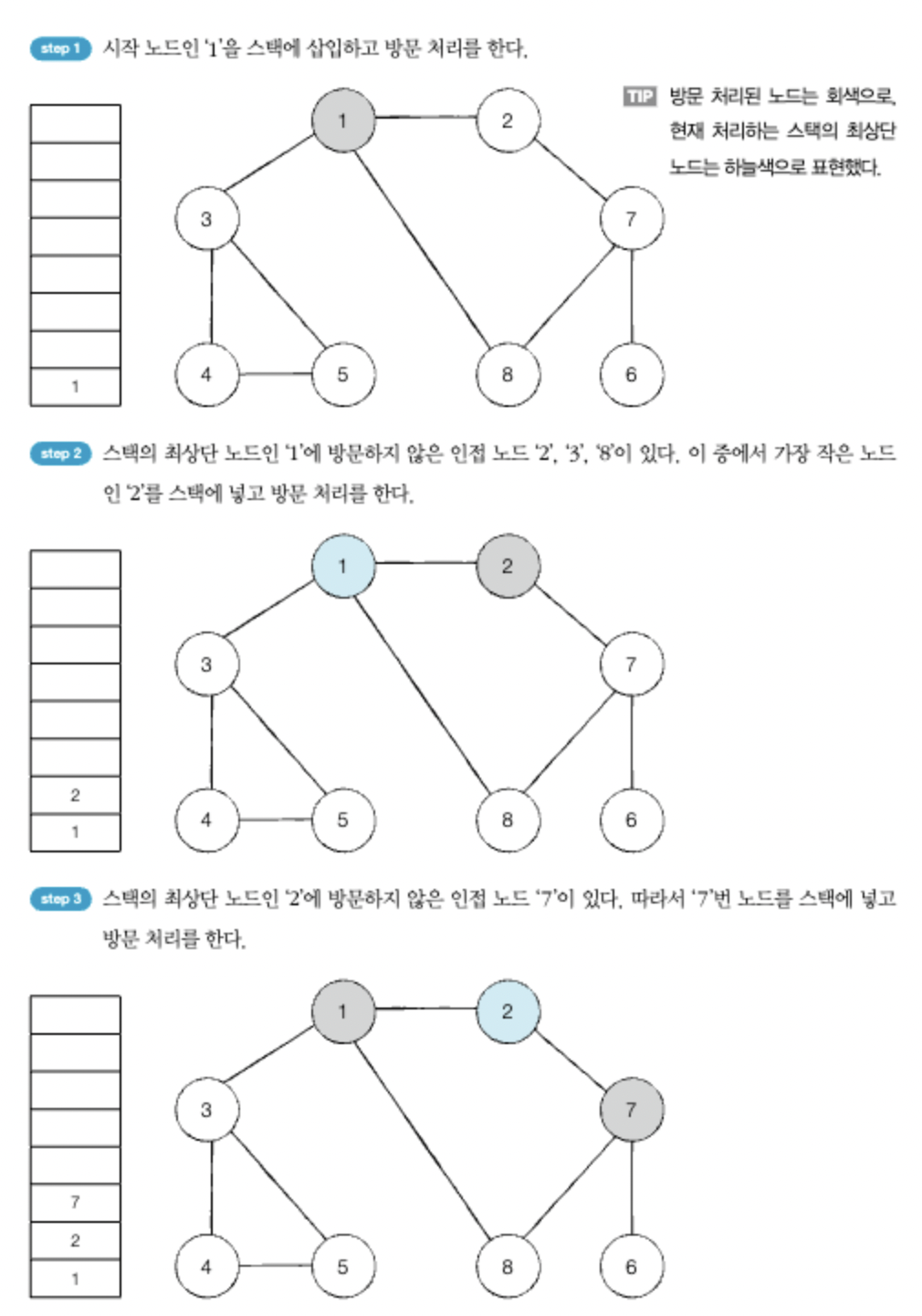




깊이 우선 탐색 알고리즘인 DFS는 스택 자료구조에 기초한다는 점에서 구현이 간단하다. 실제로는 스택을 쓰지 않아도 되며, 탐색을 수행함에 있어 데이터의 갯수가 N개인 경우 O(N)의 시간이 소요 된다는 특징이 있다. 또한, DFS는 스택을 이용하는 알고리즘이기 때문에 실제 구현은 재귀 함수를 이용하면 훨씬 간단하게 구현 가능하다. 다음은 예제 코드이다.
# DFS 예제 함수
def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end=' ')
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)
# 실행결과 : 1 2 7 6 8 3 4 5
'알고리즘' 카테고리의 다른 글
| [Algorithm]정렬(1) - 선택, 삽입 정렬 (0) | 2024.07.09 |
|---|---|
| [Algorithm]DFS/BFS(3) - BFS (0) | 2024.07.02 |
| [Algorithm] DFS/BFS(1) - DFS/BFS를 이해하기 위한 자료구조 (0) | 2024.06.29 |
| [Algorithm] "구현"이란 무엇일까? (0) | 2024.06.27 |
| [알고리즘] Greedy Algorithm(1) (0) | 2024.06.25 |