Jay's Develop Note

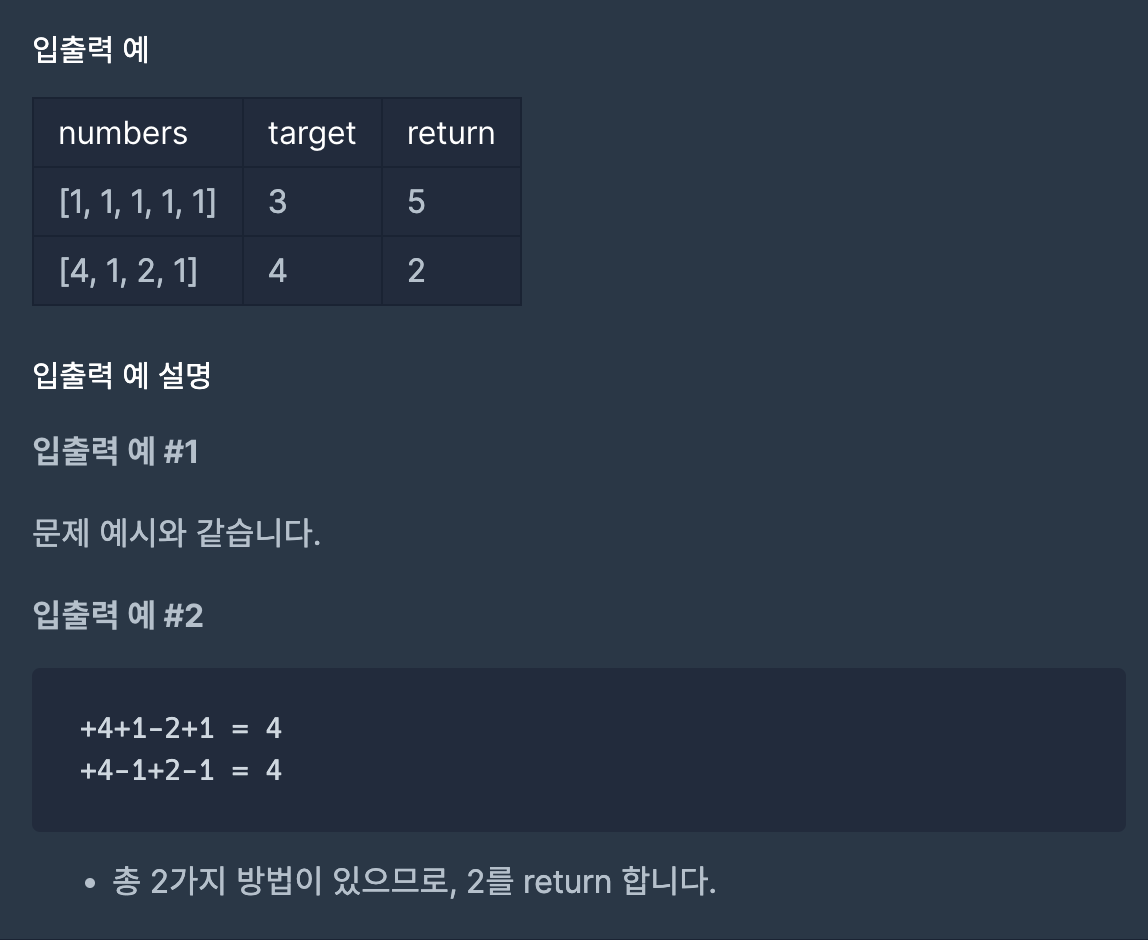
문제 :

이 문제를 보고 BFS인지 떠올릴 수 있는 요소들 :

1. 최단 변환 과정 찾기: 문제에서 요구하는 것은 ‘가장 짧은 변환 과정’을 찾는 것이다. BFS는 레벨별로 모든 가능성을 탐색하며, 이 과정에서 각 단계의 모든 가능한 경우를 고려하기 때문에 최단 경로를 보장한다.

2. 한 번에 한 글자만 바꿀 수 있는 규칙: 이 규칙은 각 단계에서 가능한 모든 변환을 시도해볼 수 있게 하며, BFS는 이러한 시도를 체계적으로 관리하여 가장 빠른 결과를 도출할 수 있게 한다.

3. words 리스트의 제한된 크기: BFS는 상대적으로 제한된 범위 내에서 효과적으로 작동한다. words의 크기가 50개 이하로 제한되어 있어, BFS를 사용할 경우 너무 많은 메모리를 소모하거나 시간이 과도하게 걸리는 문제를 피할 수 있다.

BFS는 큐, DFS는 스택, 재귀를 기반으로 동작한다. 아래 코드를 살펴보자.

from collections import deque

def solution(begin, target, words):
    if target not in words:
        return 0
    queue = deque()
    queue.append((begin, 0))
    visited = set()
    
    while queue:
        curr, steps = queue.popleft()
        if curr == target:
            return steps
        for word in words:
            if word not in visited and sum([c1 != c2 for c1, c2 in zip(curr, word)]) == 1:
                visited.add(word)
                queue.append((word, steps + 1))
    return 0

우선, 타겟이 words배열에 없으면 아예 검사 자체를 할 필요가 없으므로 맨 앞단에 이 조건문을 넣어 이 조건이 fail하면 곧바로 끝내도록 한다.

다음으로, BFS에서 사용될 큐를 만들어준다. 다음으로, 처음 검사될 단어 begin과 변환 횟수 0 을 튜플에 담아 큐에 넣어준다. 다음으로, 이미 방문한 노드(word)를 재방문 하지 않기 위한 visited를 만든다. 또한, BFS에서는 이 visited가 최단 경로를 보장 해준다. 

만약, 타겟 단어가 words배열 안에 존재한다면, while문으로 넘어간다.

while queue: 큐에 요소가 하나라도 있는동안,

큐에서 요소를 하나 꺼내어 현재 단어(curr), 몇 단계를 거쳐 단어가 변환 되었는지를 나타내는 steps 변수에 할당한다. 만약, 꺼낸 단어가 타겟과 같다면 바로 스텝을 리턴한다. 

아니라면, words의 단어들을 하나씩 순회하며 이 단어가 '방문된 적이 없고', 문제의 핵심 조건중 하나인 "단 한가지 단어만 바꿀 수 있다면"을 검사해야 한다. 두개의 단어가 철자 하나만 빼고 모두 같은지 가장 쉽고 빠르게 확인하는 방법은 문자열에 zip을 사용하는것이다. 저 짧은 if문 안에 3개의 스킬(?)이 들어갔다.

1. 리스트 컴프리헨션

2. 문자열 zip

3. True == 1, False == 0

우선, 

sum([c1 != c2 for c1, c2 in zip(curr, word)])

zip 함수를 문자열에 사용하여 두 문자열 간의 다른 문자를 찾는 방법은 매우 유용하다. 이를 통해 한 단어에서 다른 단어로의 변환이 한 글자만 다른지 쉽게 확인할 수 있다.

문자열에서의 zip 활용 예

curr = "hit", word = "hot"의 예를 들면, zip("hit", "hot")은 각 문자를 인덱스 별로 묶어서 [(h, h), (i, o), (t, t)]과 같은 튜플의 리스트를 생성한다. 이 튜플에서 첫 번째 요소는 c1, 두 번째 요소는 c2로 할당된다.

문자 비교와 리스트 컴프리헨션

리스트 컴프리헨션 c1 != c2는 각 튜플을 비교하여, 두 문자가 다르면 True, 같으면 False를 반환한다. 따라서 위 예에서는 [False, True, False] 리스트가 생성된다. 이 리스트는 각 문자 위치에서 문자가 같은지 다른지를 나타낸다.

True와 False의 수치 계산

파이썬에서는 True와 False를 각각 1과 0으로 처리할 수 있다. 이 특성 덕분에 sum([False, True, False]) 호출이 가능하며, 이는 1을 반환한다. 이는 “hit”와 “hot” 사이에 정확히 한 글자만 다름을 의미한다.

BFS에서의 활용

이 기능을 BFS 탐색에 적용할 때, 큐에서 현재 단어를 꺼내고 이와 한 글자만 다른 모든 단어를 찾아내는 과정에서 중요하게 사용된다. 만약 해당 단어가 방문하지 않은 단어이고 한 개의 문자만 다르다면, 이 단어는 방문 대상으로 간주되어 방문 기록에 추가되고, 큐에는 이 단어와 현재 단계 수에서 1을 더한 값이 함께 저장된다.

이러한 절차를 통해 BFS는 각 단계마다 가능한 모든 경로를 탐색하며, 최초로 목표 단어에 도달할 때 그 경로가 최단 경로임을 보장한다. 각 단어는 처음 방문될 때 가장 적은 수의 변환을 거쳐 도달했으므로, 이후에 같은 단어에 도달하는 다른 경로는 더 많은 변환을 필요로 하여 고려되지 않는다.

어제 최대힙을 잠깐 공부했었는데, 오늘 공부를 하다가 또 최대힙을 발견하여 최대힙을 다시 정리하면서 넘어가고자 한다.

우선, 문제를 보자.

문제를 보면, 작업량과 남은 시간을 가지고 최소한의 야근 피로도를 계산하는 문제이다. 여기서 야근 피로도는 남은 작업 시간들의 제곱으로 구해지기 때문에, 남은 시간 n 동안 가능한 한 큰 작업을 최대한 줄여서 피로도를 최소화하는 게 목표이다.

예를 들어, 주어진 작업량이 [4, 3, 3]이고 남은 시간이 4라고 하면 이 경우, 가장 큰 값인 4를 먼저 줄이는 게 효율적이다. 그래서 4를 1만큼 줄이면 남은 시간은 3이 되고, 배열은 [3, 3, 3]이 된다. 이후에도 계속 최댓값을 찾아서 1씩 줄여주는 과정을 반복한다. 예를 들어, 3을 또 줄이면 배열은 [3, 3, 2]가 되고 남은 시간은 2가 되는 식으로 진행한다.

여기서 문제가 발생하는데:

1. 매 반복마다 최댓값을 찾아야 하는데, max() 함수를 반복적으로 호출하면 성능이 떨어진다.

2. max()를 피하기 위해 정렬된 배열을 사용하려고 해도, 매번 배열을 다시 정렬해야 해서 이 방법도 비효율적이다.

따라서 최댓값을 빠르게 찾아내면서도 효율적으로 값을 줄일 수 있는 방법을 고려해야 해.

이때, 최대, 또는 최소값을 빠르게 찾아내면서 계속 트래킹 할 수 있는 자료구조는 파이썬의 heap 이 있다.

힙(Heap)은 완전 이진 트리(Complete Binary Tree) 구조를 가지는 특수한 트리 기반의 자료구조로, 최댓값 또는 최솟값을 빠르게 찾아내기 위한 구조다. 힙은 크게 최소 힙과 최대 힙으로 나뉘며, 각각 특정 조건을 만족하는 이진 트리 형태로 값을 저장한다.

1. 최소 힙(Min Heap):

• 부모 노드가 자식 노드보다 작거나 같은 값을 가진다.

• 즉, 루트(root) 노드는 항상 힙에서 가장 작은 값이다.

• 이를 통해 매번 가장 작은 값을 빠르게 꺼낼 수 있다.

• 예를 들어, [1, 3, 5, 7, 9]가 최소 힙으로 구성되어 있다면, 1이 최솟값으로 가장 위에 자리잡는다.

2. 최대 힙(Max Heap):

• 부모 노드가 자식 노드보다 크거나 같은 값을 가진다.

• 즉, 루트 노드는 항상 힙에서 가장 큰 값이다.

• 이를 통해 매번 가장 큰 값을 빠르게 꺼낼 수 있다.

• 예를 들어, [9, 7, 5, 3, 1]이 최대 힙으로 구성되어 있다면, 9가 최댓값으로 가장 위에 자리잡는다.

힙의 핵심 특징:

• 시간 복잡도: 삽입(insert)과 삭제(remove)는 O(log N)의 시간 복잡도를 가진다. 이는 트리의 높이에 해당하는 연산이기 때문이다. 힙은 트리가 완전히 채워지므로, 트리의 높이는 log N에 비례한다.

• 실시간 트래킹: 반복적으로 최댓값 또는 최솟값을 요구하는 문제에서 매우 유용하다. 힙은 트리 구조를 유지하며 값을 삽입하거나 삭제하므로 매번 정렬할 필요 없이 효율적으로 최댓값이나 최솟값을 찾을 수 있다.

파이썬에서의 힙 구현:

• 파이썬의 heapq 모듈은 기본적으로 최소 힙을 제공한다. 즉, 이 모듈을 사용하면 항상 최솟값을 빠르게 찾을 수 있다.

• 최대 힙은 별도로 제공되지 않으나, 음수 변환을 통해 간단히 구현할 수 있다. 값을 삽입할 때 음수로 변환하고, 값을 꺼낼 때 다시 양수로 변환하여 최대 힙처럼 동작하게 할 수 있다.

heapq 모듈 주요 함수:

1. heapq.heappush(heap, item): item을 힙에 추가한다.

2. heapq.heappop(heap): 힙에서 최솟값을 꺼낸다.

3. heapq.heapify(list): 주어진 리스트를 힙 구조로 변환한다.

최대 힙 예시 (파이썬에서 음수 변환을 통해 구현):

import heapq

# 최대 힙을 구현하기 위해 값의 부호를 반전

max_heap = []

heapq.heappush(max_heap, -10)  # 10을 최대 힙에 추가 (음수로)

heapq.heappush(max_heap, -30)  # 30을 최대 힙에 추가 (음수로)

heapq.heappush(max_heap, -20)  # 20을 최대 힙에 추가 (음수로)

# 최대값 꺼내기

print(-heapq.heappop(max_heap))  # 출력: 30 (음수로 저장했기 때문에 다시 양수로 바꿈)

힙의 용도:

• 우선순위 큐 구현: 항상 우선순위가 높은 작업을 먼저 처리해야 하는 경우.

• 정렬이 필요 없는 트래킹: 최댓값이나 최솟값을 자주 구하는 문제에서 매우 효율적.

• 작업 스케줄링: 작업 시간을 기준으로 우선순위를 정해 빠르게 처리를 해야 하는 스케줄링 문제에서 사용.

힙은 정렬이 반복적으로 필요할 때 매우 효율적이며, 특히 우선순위가 중요한 문제에서 자주 사용되는 자료구조이다.

그러면, 이 문제에 힙을 구현해 보자. 이 문제는, 최솟값이 아니라 최댓값을 실시간으로 트래킹 해야 하므로 최대힙을 사용해야 한다.

import heapq

def solution(n, works):
    res = 0
    works = [-x for x in works]
    heapq.heapify(works)
    
    while n > 0 and works[0] < 0:
        max_val = -heapq.heappop(works)
        max_val -= 1
        n -= 1
        heapq.heappush(works, -max_val)
    
    for i in works:
        res += pow(i, 2)
    return res

우선, import heapq를 사용해 힙을 가져온다.

그리고 최대힙을 구현하기 위해 주어진 works 배열의 각 요소를 음수로 변환한다. 이는 파이썬의 기본 힙이 최소 힙이기 때문에, 음수로 변환하여 최소 힙을 최대 힙처럼 사용할 수 있기 때문이다. 이후, heapq.heapify(works)를 사용해 음수로 변환한 works 배열을 힙 자료구조로 변환한다.

이제, while문에서:

먼저, heapq.heappop(works)를 사용해 works 힙에서 최댓값을 꺼낸다. 음수로 변환했기 때문에 음수 중 가장 작은 값이 나오지만, 우리는 이를 다시 양수로 바꿔 원래의 최댓값을 구한다.

다음으로, 꺼낸 최댓값을 1 감소시키고, 이를 다시 힙에 넣어야 한다. 이때, 다시 음수로 변환하여 넣어야 최대힙을 유지할 수 있으므로, heapq.heappush(works, -max_val)을 사용해 힙에 삽입한다.

이 과정을 반복하면, 매 반복마다 최대값이 유지되는 힙 구조를 통해 효율적으로 최댓값을 줄여 나갈 수 있다. 이 방식은 max()나 sort()를 반복해서 호출할 필요 없이 최댓값을 바로 꺼내고 수정한 뒤 다시 넣는 작업을 효율적으로 처리할 수 있다.

따라서, 최대값을 계속 유지하면서 실시간으로 값을 조정할 수 있는 장점을 이용하는 것이다.

프로그래머스를 풀다가 완전 탐색 문제를 만났다.

위 문제는 결국 모든 조합을 찾아 소수가 되는 경우를 찾아야 한다. 전형적인 완전 탐색 문제이다. 

하지만 문제가 하나 더 있다. 여기서 어떻게 모든 조합을 찾아낼 수 있을까? for문을 사용해 모든 조합을 만들면 너무 코드가 복잡해진다. 이럴땐 Python의 itertools.combinations을 사용하여 간편하게 3개의 숫자를 고를 수 있다.

import itertools
import math

def is_prime(n):
    if n < 2:
        return False
    for i in range(2, int(math.sqrt(n)) + 1):
        if n % i == 0:
            return False
    return True

def solution(nums):
    count = 0
    # 3개의 숫자를 선택하는 모든 조합 구하기
    for comb in itertools.combinations(nums, 3):
        if is_prime(sum(comb)):  # 선택한 숫자들의 합이 소수인지 확인
            count += 1
    return count

이와 같이 itertools.combinations(nums, 3)을 하면 nums 배열에서 중복을 허용하지 않는 3개의 원소를 무작위로 골라 가능한 모든 조합을 만든다.

🔒 문제 분석

알겠지만 easy 수준의 문제는 문제 분석 능력을 따로 필요로 하지 않는다. '알고리즘' 보단 어떤 '자료구조'를 쓸지만 떠올리면 되지만, 레벨 2 이상을 올라가면 자료구조, 알고리즘 모두 고려를 해야 하는 상황이기 때문에 문제 분석을 해야한다.

1. 모든 조합을 탐색해야 하는 상황

• 주어진 숫자들을 가지고 더하거나 빼서 타겟 넘버를 만들어야 한다.
• 각 숫자에 대해 - ,+ 의 옵션이 있으므로 이를 통해 가능한 모든 조합을 탐색 해야한다.
• "모든 조합을 탐색"해야 하는 문제는 보통 DFS나 BFS로 접근한다.

2. 재귀적 구조

• 각 숫자에 대해 두가지 선택지를 고려해야 하는데, 이는 재귀적으로 각 선택지를 탐색하는 구조와 유사하다.
• 특히, 특정 조건을 만족하는 모든 경로를 찾거나 모든 가능한 경로를 탐색하는 문제는 DFS로 해결하는 경우가 많다.

3. 문제의 조건

• 주어진 숫자들의 순서를 바꾸지 않고 각 숫자를 더하거나 빼서 타겟 넘버를 만드는 방법의 수를 찾아야 한다.
• 이는 각 단계마다 두 가지 선택지를 가지는 트리 구조로 생각할 수 있습니다. DFS는 트리의 모든 경로를 탐색하는 데 적합하다.

이러한 문제를 보고 DFS를 떠올리게 되는 핵심 포인트는:

• 모든 가능한 조합을 탐색해야 하는 요구사항
• 재귀적 탐색이 필요함
• 경로의 누적 합을 관리해야 함

DFS는 두 가지 방식으로 구현될 수 있다:

1. 재귀 호출을 통한 구현
2. 스택을 이용한 반복적 구현

재귀 호출 방식이 더 직관적이고 간단하기 때문에 많이 사용된다. 하지만 재귀 깊이가 깊어질 경우 스택 오버플로우 문제가 발생할 수 있으며, 이럴 때는 반복적 구현이 유용할 수 있다.

def solution(numbers, target):
    def dfs(index, current_sum):
        if index == len(numbers):
            return 1 if current_sum == target else 0
        
        add_case = dfs(index + 1, current_sum + numbers[index])
        subtract_case = dfs(index + 1, current_sum - numbers[index])
        
        return add_case + subtract_case

    return dfs(0, 0)

- 재귀적으로 호출할 dfs라는 함수를 선언 해준다. 우리가 필요한것은 target에 도달했는지 확인을 하기 위한 current_sum과 index를 파라미터로 받는다.

- 이 함수가 호출되면, 먼저 파라미터로 받은 인덱스가 현재 입력값으로 받은 numbers의 길이와 일치하는지 확인한 후(리스트에 끝에 도달했음을 의미), 만약 현재 리스트 끝에 도달했고, current_sum이 target과 일치한다면 1을 반환하고, 그렇지 않다면 0을 반환한다. 여기서 1을 반환하는건 경우의 수 카운트 +1 이라고 생각하면 쉽다.

-다음으로, 2가지의 케이스(+, -)를 담당할 재귀문을 작성 해준다.

- add_case는 다음 인덱스와 현재까지의 합에서 현재 검사중인 요소를  '더해' 재귀문을 호출한다.

- subtract_case는 다음 인덱스와 현재까지의 합에서 현재 검사중인 요소를 '빼서' 재귀문을 호출한다.

🔍 재귀...백트래킹... 하아

글을 쓰다 보니 작년 자구알고 수업때 재귀를 공부하다가 고통받았던 기억이 나 다시 한번 재귀 + 백트래킹을 좀 더 자세히 살펴보고 넘어 가보자.

재귀 함수 호출은 실제로 함수 호출 스택에 쌓인다. 각 재귀 호출은 함수 호출 스택에 새로운 프레임을 추가하고, 해당 호출이 완료되면 스택에서 제거(pop)된다. 이 과정은 재귀 호출이 진행되는 동안 함수 호출 순서와 현재 상태를 관리하는 데 사용된다.

 재귀 함수의 스택 동작

예를 들어, `numbers = [1, 1, 1, 1, 1]`이고 `target = 3`인 경우를 다시 살펴보자.

재귀 호출 순서와 스택 동작

1. 초기 호출: `dfs(0, 0)` 호출:
   - `index = 0`, `curr_sum = 0`
   - 호출 스택: `[dfs(0, 0)]`

2. 첫 번째 숫자에 대해:
   - `add_case = dfs(1, 1)` 호출:
     - `index = 1`, `curr_sum = 1`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1)]`

3. 두 번째 숫자에 대해:
   - `add_case = dfs(2, 2)` 호출:
     - `index = 2`, `curr_sum = 2`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2)]`

4. 세 번째 숫자에 대해:
   - `add_case = dfs(3, 3)` 호출:
     - `index = 3`, `curr_sum = 3`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3)]`

5. 네 번째 숫자에 대해:
   - `add_case = dfs(4, 4)` 호출:
     - `index = 4`, `curr_sum = 4`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3), dfs(4, 4)]`

6. 다섯 번째 숫자에 대해:
   - `add_case = dfs(5, 5)` 호출:
     - `index = 5`, `curr_sum = 5`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3), dfs(4, 4), dfs(5, 5)]`
     - 조건 `index == len(numbers)`이 참이므로, `curr_sum == target`를 확인하고, `0`을 반환.
     - 스택에서 `dfs(5, 5)`가 제거되고, `dfs(4, 4)`로 돌아감.
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3), dfs(4, 4)]`

7. 백트래킹: 
   - `dfs(4, 4)`에서 `subtract_case = dfs(5, 3)` 호출:
     - `index = 5`, `curr_sum = 3`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3), dfs(4, 4), dfs(5, 3)]`
     - 조건 `index == len(numbers)`이 참이므로, `curr_sum == target`를 확인하고, `1`을 반환.
     - 스택에서 `dfs(5, 3)`가 제거되고, `dfs(4, 4)`로 돌아감.
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3), dfs(4, 4)]`
     - `dfs(4, 4)`에서 `add_case + subtract_case = 0 + 1 = 1` 반환.
     - 스택에서 `dfs(4, 4)`가 제거되고, `dfs(3, 3)`로 돌아감.
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3)]`

8. 세 번째 숫자에 대해:
   - `dfs(3, 3)`에서 `subtract_case = dfs(4, 2)` 호출:
     - `index = 4`, `curr_sum = 2`
     - 호출 스택: `[dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3), dfs(4, 2)]`

이와 같은 방식으로 재귀 호출은 계속해서 스택에 쌓이고, 기저 조건에 도달하면 반환하면서 스택에서 제거된다. 

요약

- 재귀 호출 스택: 각 함수 호출은 스택에 쌓인다. 재귀 호출이 반환될 때마다 스택에서 제거된다.
- 백트래킹: 한 경로의 탐색이 끝나면(재귀 호출이 반환되면) 스택에서 제거되고, 이전 호출로 돌아가서 다음 경로를 탐색한다.
- 함수 호출 순서: 각 함수 호출은 순차적으로 진행되며, 호출이 완료되면 스택에서 제거되고, 다음 경로를 탐색하기 위해 이전 상태로 돌아간다.

가장 먼저 해야 할것은 어떤 알고리즘, 자료구조를 사용할지 파악을 하는 것이다.

1. 문제 유형 파악

• 맵을 통한 경로 탐색 : 2차원 격자 맵에서 목표 지점까지의 경로를 찾는 문제이다.
• 최단 경로 요구 : 문제는 "최단 경로"를 찾는것을 요구한다.

2. 그래프 탐색 문제 인식

• 격자 맵 : 격자 맵에서 각 칸은 노드, 이동은 간선으로 볼 수 있다. 즉, 이 문제는 그래프 탐색 문제로 바라볼 수 있다.
• 무가중치 그래프 : 각 이동은 동일한 비용(칸을 한 칸 이동하는 비율은 동일)이다. 가중치가 없는 그래프로 볼 수 있다.

3. 최단 경로 탐색 요구

• 최단 경로 보장 :  문제에서의 요구 사항은 목적지 까지의 최단 경로를 찾는 것이다.
• 무가중치 그래프의 최단 경로 : 무가중치 그래프에서 최단 경로를 찾기 위한 가장 효율적인 알고리즘은 BFS이다. BFS는 먼저 방문한 경로가 최단 경로임을 보장한다.

아래는 제출해 통과한 코드이다.

from collections import deque

def solution(maps):
    directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
    
    n = len(maps)
    m = len(maps[0])
    
    queue = deque([(0,0,1)])
    visited = [[False] * m for _ in range(n)]
    visited[0][0] = True
    
    while queue:
        x, y, distance = queue.popleft()
        
        if x == n - 1 and y == m - 1:
            return distance
        
        for dx, dy in directions:
            nx, ny = x + dx, y + dy
            
            if 0 <= nx < n and 0 <= ny < m and maps[nx][ny] == 1 and not visited[nx][ny]:
                queue.append((nx, ny, distance + 1))
                visited[nx][ny] = True
    return -1

- BFS는 큐를 사용해 인접한 모든 노드를 방문하는 방식이다. 큐를 사용하기 위해 from collections import deque를 해 준다.

- 다음으로, 한 노드(격자에서는 현재 서있는 위치)에서 한칸씩 갈 수 있는 모든 방향을 담은 directions 배열을 선언하고 초기화 한다.

동, 서 , 남, 북 으로 총 4가지의 경우가 있으므로 (1, 0)[동] // (-1, 0)[서] // (0, 1)[남] // (0, -1)[북] 과 같이 지정 해준다.

- 또한, 입력값으로 주어진 maps의 크기를 구하기 위해 행, 열의 길이를 각각 n, m에 매핑 시켜준다.

- 다음으로 , 큐를 선언해주고 [0, 0, 1]의 값을 비어있는 큐에 넣어준다. 여기서는 (x, y, distance)인데, 즉 맨 처음의 좌표는 (0,0)이고, 여기서는 시작 지점 자체도 포함한 이동 칸의 수를 계산해야 하므로 초기 거리를 1로 설정한다.

- 다음으로, 방문 여부를 확인하는 2차원 배열 visited를 선언 해준다. 이 2차원 배열의 초기 상태는 n * m 만큼의 2차원 배열에 False로 채워넣어 아직 방문하지 않았다는걸 의미한다.

- 첫번째 시작점은 이미 방문했으므로 visited[0][0] = True로 설정한다.

- 이제, 위에서 선언한 큐에 요소가 없을때까지 다음 while문을 반복한다.

- 큐에서 요소 하나를 꺼낸다. 요소를 꺼내어 각각 x, y, distance에 할당한다.

- 만약, 이미 끝 지점에 도달했다면(if x == n - 1 and y == m - 1) 현재까지 저장된 거리를 리턴하고 끝낸다.

- 아직 끝에 도달하지 않았다면, 위에서 선언한 동 서 남 북의 값이 담긴 directions 배열을 순회한다.

- 예를 들어보자. 현재 큐에 있는 값은 (0,0,1)이고, 이 0, 0, 1은 각각 x, y distance에 매핑된다. 아직 현재 값은 끝에 도달하지 않았으므로 첫번째 if문은 통과되고, 다음으로 directions에 있는 동쪽 값(1, 0)을 꺼내 현재 위치에서(0, 0, 1) 동쪽으로 한칸 이동한다. 이렇게 되면 nx, ny에는 1, 0이 담길 것이다.

- 다음으로, 이렇게 업데이트 된 값을 가지고 유효성을 검사한다. 여기서의 유효성이란, maps의 범위를 벗어나지 않았는지, 즉, 처음 입력값으로 주어진 n x m 격자 배열의 범위에서 벗어나지 않는지(if 0 <= nx < n and 0 <= ny < m), 또 문제에서 1은 갈 수 있는 노드, 0은 갈 수 없는 막힌 노드로 설정이 되어 있으므로, 가려는 칸이 1인지(갈 수 있는 노드인지) 판별을 해야한다.(and maps[nx][ny] == 1) 또한, 이미 방문한 노드라면 다시 방문하지 않아도 되므로 not visited[nx][ny]를 통해 방문한적 있는지 없는지를 검사한다.

-예를 들어보자. 위의 예시에서의 입력값을 기준으로 동쪽으로 가려고 한다면 and maps[nx][ny] == 1 여기서 False를 반환할것이다. 다음은 현재 노드의 서쪽을 검사하는데, 서쪽은 maps의 범위를 벗어나므로 여기서도 false를 반환 할 것이다. 다음으로, 남쪽을 검사할땐, 남쪽은 현재 maps의 범위를 벗어나지 않고, 노드의 값은 1이고, 아직 방문한적이 없으므로 큐에 업데이트 된 값을 넣어준다. 여기서는 

queue.append(nx, ny, distance + 1)를 하여 현재 이동한 노드의 좌표와 현재까지 이동한 거리를 넣어준다. 이 문제에서는 한번에 한 칸씩 이동하므로 distance + 1을 해주면 된다. 또한 이 노드는 이제 방문한 노드가 되므로 visited또한 True로 해줘야 한다.

여기서 궁금한 점이 생겼다. 로직 자체는 현재 검사중인 노드에서 동 서 남 북의 위치를 각각 검사하여 갈 수 있다면 그 노드를 큐에 넣고 같은 작업을 반복하는데, 이게 어떻게 최단 거리를 도출 할 수 있지?

다음은 GPT에게서 얻어낸 답변이다!

이 과정을 계속 반복하면, 최단 경로로 목표 지점 (4, 4)에 도달하게 됩니다. BFS는 현재 위치에서 가능한 모든 경로를 탐색하기 때문에, 먼저 도달한 경로가 최단 경로임을 보장합니다.

from collections import deque

def solution(maps):
    directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
    n, m = len(maps), len(maps[0])
    queue = deque([(0, 0, 1)])
    visited = [[False] * m for _ in range(n)]
    visited[0][0] = True

    while queue:
        x, y, distance = queue.popleft()
        if x == n - 1 and y == m - 1:
            return distance
        
        for dx, dy in directions:
            nx, ny = x + dx, y + dy
            if 0 <= nx < n and 0 <= ny < m and maps[nx][ny] == 1 and not visited[nx][ny]:
                queue.append((nx, ny, distance + 1))
                visited[nx][ny] = True

    return -1

# 예시 테스트
maps1 = [[1,0,1,1,1], [1,0,1,0,1], [1,0,1,1,1], [1,1,1,0,1], [0,0,0,0,1]]
maps2 = [[1,0,1,1,1], [1,0,1,0,1], [1,0,1,1,1], [1,1,1,0,0], [0,0,0,0,1]]
print(solution(maps1))  # 출력: 11
print(solution(maps2))  # 출력: -1

- 문제를 보면 각 요소의 출현 횟수와 배열을 한번에 10칸씩 검사하며 확인을 해야한다. 그래서 Counter와 sliding window가 생각났다.

from collections import Counter

def solution(want, number, discount):
    stuff_dict = {}
    days = 10
    res = 0
    
    for i in range(len(want)):
        stuff_dict[want[i]] = number[i]
        
    for i in range(len(discount) - days + 1):
        counts = Counter(discount[i:i+days])
        
        if all(counts[key] >= val for key, val in stuff_dict.items()):
            res += 1
    return res

-우선, Counter를 이용하기 위해 from collections import Counter를 해준다.

- 그리고 선언한 딕셔너리에 원하는 물건과 원하는 갯수를 매핑 해준다.

- 여기서 sliding window를 사용했는데, discount배열에서 이제 각 루프를 돌 때마다 10개씩 한번에 출현 횟수를 세어야 한다. 

"all"

`all` 함수는 파이썬 내장 함수로, 반복 가능한(iterable) 객체의 모든 요소가 참(True)인 경우에만 `True`를 반환합니다. 그렇지 않으면 `False`를 반환합니다. 일반적으로 리스트, 튜플, 세트, 딕셔너리 등과 같은 반복 가능한 객체에서 사용됩니다.

기본 사용법

all(iterable)

- `iterable`: 리스트, 튜플, 세트, 딕셔너리 등 반복 가능한 객체.

예제

1. 리스트의 모든 요소가 참인지 확인

# 모든 요소가 참일 때
print(all([True, True, True]))  # Output: True

# 하나라도 거짓이 있을 때
print(all([True, False, True]))  # Output: False

# 빈 리스트 (빈 반복 가능한 객체는 항상 True를 반환)
print(all([]))  # Output: True

2. 문자열의 모든 문자가 알파벳인지 확인

words = ["apple", "banana", "cherry"]

# 모든 단어가 알파벳 문자로만 구성되어 있는지 확인
print(all(word.isalpha() for word in words))  # Output: True

# 문자열 중 하나가 숫자를 포함할 때
words = ["apple", "banana", "cherry123"]
print(all(word.isalpha() for word in words))  # Output: False

3. 딕셔너리 값이 모두 양수인지 확인

scores = {"math": 90, "science": 85, "english": 88}

# 모든 점수가 양수인지 확인
print(all(score > 0 for score in scores.values()))  # Output: True

# 점수 중 하나가 음수일 때
scores = {"math": 90, "science": -85, "english": 88}
print(all(score > 0 for score in scores.values()))  # Output: False

설명

- `all(counts[key] >= val for key, val in stuff_dict.items())`:
  - `stuff_dict.items()`는 (key, value) 쌍을 반환합니다.
  - `counts[key] >= val`은 현재 윈도우 내의 제품 수량이 원하는 수량 이상인지를 확인합니다.
  - `all` 함수는 이러한 조건이 모든 제품에 대해 참인지 확인합니다. 모든 조건이 참이면 `True`를 반환하고, 그렇지 않으면 `False`를 반환합니다.

- 문제를 보고 Counter가 바로 생각났다. 입력값이 리스트로 주어지고, 그 리스트에서 각 요소의 출현 횟수를 알고자 할땐 Counter를 쓰면 편하다. 

from collections import Counter 

def solution(k, tangerine):
    res = 0
    temp = 0
    counter = Counter(tangerine)
    sorted_count = counter.most_common()
    
    for item, count in sorted_count:
        if temp < k:
            res += 1
            temp += count
    return res

- counter = Counter(tangerine)은 tangerine리스트에 담긴 요소들의 출현 횟수를 딕셔너리 형식으로 저장 할 것이다. 예를 들어, 주어진 리스트가 [1, 3, 2, 5, 4, 5, 2, 3]라면 counter 변수에는 {3: 2, 2: 2, 5: 2, 1: 1, 4: 1} 와 같이 저장된다. 이 결과는 Counter 객체의 요소를 저장하는 방식이다. Counter는 요소를 키로, 빈도를 값으로 가지는 딕셔너리 형태로 저장한다.

- 다음으로, 우리가 하고 싶은건 k보다 작은 만큼 귤의 종류를 리턴 하는것이기 때문에 리스트를 순회하며 검사 할 수 있도록 정렬을 해주었다. counter.most_common() 메서드는 현재 저장된 키:출현횟수 쌍에서 출현 횟수를 기준으로 정렬을 수행한다. 단, 여기서의 정렬은 오름차순 정렬이 아니라 이름 그대로(most_common은 '가장 흔한'이다) 가장 많이 나온 순서대로 내림차순 정렬을 수행한다. 이렇게 되면 위의 예시에서 [(3, 2), (2, 2), (5, 2), (1, 1), (4, 1)] 이렇게 리스트 안에 튜플 형태로 반환한다.

- 이렇게 하면 이제 이 정렬된 리스트를 k보다 작을때까지 순회하면 된다.

- for item, count in sorted_count는 sorted_count에 저장된 (키:출현 횟수)를 각각 item, count에 할당한다. 

- 반복문을 순회하며 현재 값이 k보다 작은지 확인 한 후, 작으면 계속하고, 아니라면 return을 하고 함수를 끝낸다

문제 : 

- 문제를 보면 주어진 문자열에서 짝을 지어야 한다는 말을 보고 '스택'이 생각났다.

def solution(s):
    stk = []
    
    for i in range(len(s)):
        if not stk:
            stk.append(s[i])
            continue
        
        if stk[-1] != s[i]:
            stk.append(s[i])
            continue
        
        if stk[-1] == s[i]:
            stk.pop()
            continue
    
    if stk:
        return 0
    else:
        return 1

우선, 빈 스택을 하나 만들어 준다.

- for문으로 입력값으로 주어진 문자열을 하나씩 순회하며

- 스택 안에 아무 값도 없다면,  스택에 현재 검사중인 문자를 넣어준다.

- 그리고 continue를 이용해 다음 루프로 넘어간다.

- 스택 안에 무언가 있다면, 현재 스택의 맨 윗값과 현재 검사중인 요쇼가 같은지 확인한다.

- 같지 않다면, 현재 검사중인 요소를 스택에 넣어준다.

- 그리고 continue를 통해 다음 루프로 넘어간다.

- 스택 안에 무언가 있고, 현재 값과 스택의 맨 위의 값이 같다면(문제에서 요구하는 짝을 지을 수 있는 경우),

- 현재 스택의 맨 위의 값을 추출한 후, 바로 다음 루프로 넘어간다.

이제 모든 for문이 끝나고, 마지막에 스택에 요소가 남아있다면(짝을 지어 문자열을 비우지 못한 경우) 0을 리턴하고 아니라면 1을 리턴한다.